Mu Yuan
笔记-1
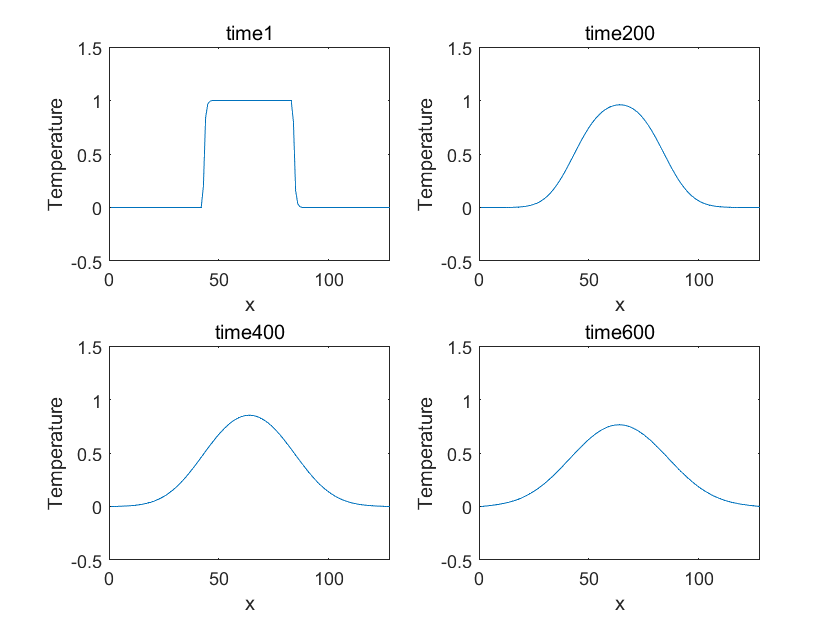
One-Dimensional Transient Heat Conduction: A Solution with Finite Difference Algorithm
MATLAB实现
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 1D transient heat conduction %
% space discretization: finite- %
% difference time integration: %
% Explicit Euler %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%-- get initial wall time:
time0 = clock();
%-- Simulation cell parameters:
Nx = 128; % 定义网格数
dx = 1.0; % 空间步长
%-- Time integration parameters:
nstep = 600; % 时间步
nprint = 200; % 绘图间隔
dtime = 0.2; % 时间步长
%-- Initialize temperature filed & grid:初始场
for i = 1:Nx
u0(i) = 0.0;
x(i) = i*dx;
%-- 定义初始热区
if((i>=44) && (i<=84))
u0(i) = 1.0;
end
end
%-- 时间推进-显式欧拉
%-- Evolve temperature field:
%--
ncount = 0;
for istep = 1:nstep
for i = 2:Nx-1 % 边界i=1，i=Nx没有更新，相当于固定边界
u0(i) = u0(i)+dtime*(u0(i+1)-2.0*u0(i)+u0(i-1))...
/(dx*dx)
end
%-- Display results:
if((mod(istep,nprint) == 0) || (istep == 1))
% istep除nprint余数为0，即istep为了print整数 或 istep == 1即初始
ncount = ncount+1;
subplot(2,2,ncount);
plot(x,u0);
time=sprintf('%d',istep);
title(['time' time]);
axis([0 Nx -0.5 1.5]);
xlabel('x');
ylabel('Temperature');
end %if
end %istep
compute_time = etime(clock(),time0);
fprintf('Compute Time: %5d\n',compute_time);运行结果：
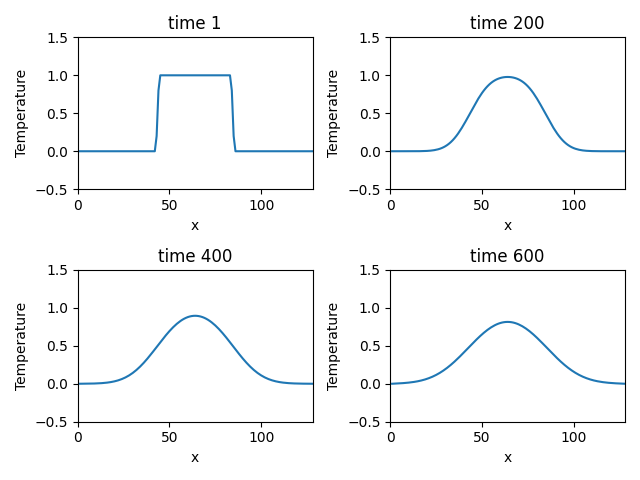
Python实现
import numpy as np
import matplotlib.pyplot as plt
import time
# 获取初始时间
time0 = time.time() # 获取当前时间戳
# 模拟单元参数
Nx = 128
dx = 1.0
# 时间积分参数
nstep = 600
nprint = 200
dtime = 0.2
# 初始化温度场和网格
u0 = np.zeros(Nx) # 创建一个长度为Nx的全零数组，储存温度值
x = np.arange(1, Nx+1)*dx # 创建空间坐标数组，从dx到Nx*dx，步长dx；np.arange(1,Nx+1)生成1到Nx+1的整数序列，乘以dx得到实际空间坐标
# 定义初始热区
u0[43:84] = 1.0 # 将索引43到83的温度设为1.0注意不包括84
# 时间推进-显式欧拉法
ncount = 0
for istep in range(1, nstep+1):
u0[1:-1] = u0[1:-1]+dtime*(u0[2:]-2.0*u0[1:-1]+u0[:-2]/(dx*dx))
# u0[1:-1]：表示除了第一个和最后一个点（边界）之外的所有点
# u0[2:]：表示从第二个点到最后一个点，比u0[1:-1]超前一个位置
# u0[:-2]：表示从第一个点到倒数第二个点（比 u0 [1:-1] 滞后一个位置）
if istep % nprint == 0 or istep == 1:
ncount += 1
plt.subplot(2,2,ncount)
plt.plot(x,u0)
plt.title(f'time {istep}')
plt.axis([0,Nx,-0.5,1.5])
plt.xlabel('x')
plt.ylabel('Temperature')
compute_time = time.time()-time0
print(f'Compute Time: {compute_time:.2f} seconds')
plt.tight_layout()
plt.show()运行结果：
Simulation of the spinodal decomposition of a binary alloy with explict Euler finite-difference algorithm
MATLAB实现
fd_ch_v1.m
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% %
%FINEITE-DIFFIRENCE PHASE-FIELD %
% CODE FOR SOLVING %
% CAHN-HILLIARD EQUATION %
% %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% get intial wall time:
% 获取初始wall时间
time0 = clock();
format long;
out2 = fopen('time_energ.out','w'); % 打开一个文件用于写入时间和能量数据
%% Simulation cell parameters:
% 模拟单元格参数
Nx = 64;
Ny = 64;
NxNy = Nx*Ny;
dx = 1.0;
dy = 1.0;
%% Time integration parameters:
nstep = 10000;
nprint = 50;
dtime = 0.01;
ttime = 0.0;
%% Material specific Parameters:
c0 = 0.40;
mobility = 1.0;
grad_coef = 0.5;
%% prepare microstructure:
iflag = 1;
[con] = micro_ch_pre(Nx,Ny,c0,iflag); % 调用函数生成初始浓度场
%% Evolve
for istep = 1:nstep
ttime = ttime+dtime;
for i = 1:Nx
for j = 1:Ny
% 定义相邻网格点（用于周期性边界条件）
jp = j+1;
jm = j-1;
ip = i+1;
im = i-1;
jp = j+1;
jm = j-1;
ip = i+1;
im = i-1;
% 应用周期性边界条件
if(im == 0)
im = Nx; % 左边界外的点等于右边界点
end
if(ip == (Nx+1))
ip = 1; % 右边界外的点等于左边界点
end
if(jm == 0)
jm = Ny; % 下边界外的点等于上边界点
end
if(jp == (Ny+1))
jp = 1; % 上边界外的点等于下边界点
end
% 获取当前点和相邻点的浓度值
hne = con(ip,j); % 右邻点
hnw = con(im,j); % 左邻点
hns = con(i,jm); % 下邻点
hnn = con(i,jp); % 上邻点
hnc = con(i,j); % 当前点
% 计算浓度场的拉普拉斯（二阶导数）
lap_con(i,j) = (hnw+hne+hns+hnn-4.0*hnc)/(dx*dy);
%% derivative of free energy:
[dfdcon] = free_energ_ch_v1(i,j,con);
% 调用函数计算自由能导数
dummy(i,j) = dfdcon-grad_coef*lap_con(i,j);
% 计算Cahn-Hilliard方程中的一项：自由能导数减去梯度项
end % for j
end % for i
%%
for i = 1:Nx
for j = 1:Ny
jp = j+1;
jm = j-1;
ip = i+1;
im = i -1;
jp = j+1;
jm = j-1;
ip = i+1;
im = i-1;
if(im == 0)
im = Nx;
end
if(ip == (Nx+1))
ip = 1;
end
if(jm == 0)
jm = Ny;
end
if(jp == (Ny+1))
jp = 1;
end
hne = con(ip,j);
hnw = con(im,j);
hns = con(i,jm);
hnn = con(i,jp);
hnc = con(i,j);
lap_dummy(i,j) = (hnw+hne+hns+hnn-4.0*hnc)/(dx*dy);
%% time integration:
% Cahn-Hilliard方程：dc/dt = M * ∇²(δF/δc - κ∇²c)
con(i,j) = con(i,j)+dtime*mobility*lap_dummy(i,j);
%% for small deviations:
% 限制浓度值在合理范围内
if(con(i,j) >= 0.9999)
con(i,j) = 0.9999;
end
if(con(i,j) < 0.00001)
con(i,j) = 0.00001;
end
end % j
end % i
%% print results
if((mod(istep,nprint) == 0 || (istep == 1)))
fprintf('done step: %5d\n',istep);
%fname1 = sprintf('time_%d.out',istep);
%out1 = fopen(fname1,"w");
%for i = 1:Nx
%for j = 1:Ny
%fprintf(out1,'%5d %5d %14.6e\n',i,j,con(i,j));
%end
%end
%fclose(out1);
%% write vtk file:
%% calculate total energy
[energ] = calculate_energ(Nx,Ny,con,grad_coef);
fprintf(out2,'%14e %14.6e\n',ttime,con,grad_coef);
write_vtk_grid_values(Nx,Ny,dx,dy,istep,con);
end % if
end % istep
%% calculate compute time:
compute_time = etime(clock(),time0);
fprintf('Compute Time: %10d\n',compute_time);micro_ch_pre.m
% 初始条件生成
function[con] = micro_ch_pre(Nx,Ny,c0,iflag)
format long;
NxNy = Nx*Ny;
noise = 0.02;
if(iflag == 1) % 2D
for i = 1:Nx
for j = 1:Ny
con(i,j) = c0+noise*(0.5-rand); % rand用于生成[0,1)的均匀随机数
end
end
else % 1D
con = zeros(NxNy,1);
for i = 1:Nx
for j = 1:Ny
ii = (i-1)*Nx+j; % 2D网格映射为1D下标
con(ii) = c0+noise*(0.5-rand);
end
end
end % if
end % endfunctioncalculate_energ.m
function [energ] = calculate_energ(Nx,Ny,con,grad_coef)
format long;
energ =0.0;
for i=1:Nx-1
ip = i + 1;
for j=1:Ny-1
jp = j + 1;
energ = energ + con(i,j)^2*(1.0-con(i,j))^2 + ...
0.5*grad_coef*((con(ip,j)-con(i,j))^2 + (con(i,jp)-con(i,j))^2);
end
end
end %endfunctionfree_energ_ch.m
% 自由能密度对浓度的导数
function [dfdcon] =free_energ_ch_v1(i,j,con)
format long;
A=1.0;
dfdcon =A*(2.0*con(i,j)*(1-con(i,j))^2-2.0*con(i,j)^2 * (1.0-con(i,j)));
% f(c)=A*c^2*(1-c)^2
% f'(c)=A*[2*c*(1-c)^2+c^2*(-2)*(1-c)]=A*[2*c*(1-c)^2-2*c^2*(1-c)]
end %endfunctionwrite_vtk_grid_values.m
function [ ]= write_vtk_grid_values(nx,ny,dx,dy,istep,data1) % [ ]表示无返回
format long
%-- open output file
fname=sprintf('time_%d.vtk',istep);
out =fopen(fname,'w'); % 'w'覆盖写入
nz=1;
npoin =nx*ny*nz;
% start writing ASCII VTK file:
% header of VTK file
% VTK文件文件头写入
fprintf(out,'# vtk DataFile Version 2.0\n');
fprintf(out,'time_10.vtk\n');
fprintf(out,'ASCII\n');
fprintf(out,'DATASET STRUCTURED_GRID\n');
%--- coords of grid points:
fprintf(out,'DIMENSIONS %5d %5d %5d\n',nx,ny,nz); % 声明网格维度
fprintf(out,'POINTS %7d float\n',npoin); % 声明节点总数
for i = 1:nx
for j = 1:ny
x =(i-1)*dx;
y =(j-1)*dy;
z = 0.0;
fprintf(out, '%14.6e %14.6e %14.6e\n',x,y,z); % 14.6e输出为14字符的6位小数的科学计数法
end
end
%--- write grid point values:
fprintf(out,'POINT_DATA %5d\n',npoin);
fprintf(out,'SCALARS CON float 1\n'); % 数据组件数 1表示标量，3表示矢量
fprintf(out,'LOOKUP_TABLE default\n'); % 颜色映射设为默认
for i = 1:nx
for j = 1:ny
ii=(i-1)*nx+j;
fprintf(out,'%14.6e\n',data1(i,j));
end
end
fclose(out);
end %endfunctionlaplacian.m
function [grad] =laplacian(nx,ny,dx,dy)
format long;
nxny=nx*ny;
r=zeros(1,nx);
r(1:2)=[2,-1]; % 定义r(1)=2, r(2)=-1, 其余为0
T=toeplitz(r); % Toeplitz矩阵，对角元素相等
E=speye(nx); % 生成稀疏单位矩阵（仅对角为1，其余为0）
grad=-(kron(T,E)+kron(E,T));
% 克罗内克积 kron(T,E)为x方向拉普拉斯矩阵2D拓展 kron(E,T)为y方向拉普拉斯矩阵2D拓展
%-- for periodic boundaries
% 添加周期性边界条件
for i=1:nx
ii=(i-1)*nx+1;
jj=ii+nx-1;
grad(ii,jj)=1.0; % 定义左边界的右临点为右边界
grad(jj,ii)=1.0; % 定义右边界的左临点为左边界
kk=nxny-nx+i;
grad(i,kk)=1.0;
grad(kk,i)=1.0;
end
grad = grad /(dx*dy); % 除以网格步长乘积以修正导数量纲
end %endfunctionPython实现
fd_cd_v1.py
import numpy as np
import time
from calculate_energ import calculate_energ
from laplacian import laplacian
from micro_ch_pre import micro_ch_pre
from write_vtk_grid_values import write_vtk_grid_values
from free_energ_ch_v1 import free_energ_ch_v1
def main():
time0 = time.time() # time.time()返回当前时间戳
out2 = open('time_energ.out','w')
Nx = 64
Ny = 64
NxNy = Nx * Ny
dx = 1.0
dy = 1.0
nstep = 10000
nprint = 50
dtime = 0.01
ttime = 0.0
c0 = 0.40
mobility = 1.0
grad_coef = 0.5
iflag = 1
con = micro_ch_pre(Nx,Ny,c0,iflag)
lap_con = np.zeros((Nx,Ny)) # 储存浓度差的拉普拉斯结果
dummy = np.zeros((Nx,Ny)) # 临时数组
lap_dummy = np.zeros((Nx,Ny)) #储存临时数组的拉普拉斯结果
for istep in range(1,nstep+1): # 时间循环，从1到nstep（包含nstep）
ttime = ttime + dtime
# 计算浓度场的拉普拉斯和自由能导数
# 双重循环遍历所有网格点
for i in range(Nx):
for j in range(Ny):
jp = j + 1
jm = j - 1
ip = i + 1
im = i - 1
if im == -1: # 左边界外
im = Nx - 1 # 循环到右边界
if ip == Nx: # 右边界外
ip = 0 #循环到左边界
if jm == -1: # 下边界外
jm = Ny - 1 # 循环到上边界
if jp == Ny: # 上边界外
jp = 0 # 循环到下边界
hne = con[ip,j] # 右临点
hnw = con[im,j] # 左临点
hns = con[i,jm] # 下临点
hnn = con[i,jp] # 上临点
hnc = con[i,j] # 当前点
lap_con[i,j] = (hnw + hne + hns + hnn - 4.0 * hnc) / (dx * dy)
# 计算拉普拉斯算子（二阶导数近似）
dfdcon = free_energ_ch_v1(i,j,con)
# 计算自由能对浓度的导数
dummy[i,j] = dfdcon - grad_coef * lap_con[i,j]
# 计算临时变量dummy
# 计算dummy的拉普拉斯并更新浓度场
for i in range(Nx):
for j in range(Ny):
jp = j + 1
jm = j - 1
ip = i + 1
im = i - 1
if im == -1:
im = Nx - 1
if ip == Nx:
ip = 0
if jm == -1:
jm = Ny - 1
if jp == Ny:
jp = 0
hne = dummy[ip,j]
hnw = dummy[im,j]
hns = dummy[i,jm]
hnn = dummy[i,jp]
hnc = dummy[i,j]
lap_dummy[i,j] = (hnw + hne + hns + hnn - 4.0 * hnc) / (dx * dy)
# 更新浓度场（Cahn-Hilliard方程的时间推进）
con[i,j] = con[i,j] + dtime * mobility * lap_dummy[i,j]
if con[i,j] >= 0.9999:
con[i,j] = 0.9999
if con[i,j] < 0.00001:
con[i,j] = 0.00001
if(istep % nprint == 0) or (istep == 1):
print(f'done step: {istep:5d}')
energ = calculate_energ(Nx,Ny,con,grad_coef)
out2.write(f'{ttime:14e} {energ:14.6e}\n')
write_vtk_grid_values(Nx,Ny,dx,dy,istep,con)
compute_time = time.time() - time0
print(f'Compute Time: {compute_time:10.0f}')
out2.close
if __name__ == "__main__":
main()micro_ch_pre.py
import numpy as np
def micro_ch_pre(Nx,Ny,c0,iflag):
NxNy = Nx * Ny
noise = 0.02
if iflag == 1:
con = np.zeros((Nx,Ny))
for i in range(Nx):
for j in range(Ny):
# 初始化浓度：平均浓度c0加上随机扰动
# np.random.rand()生成[0,1)之间的随机数
# (0.5 - np.random.rand())使随机扰动在[-0.5, 0.5)之间
# 乘以noise后，扰动范围变为[-0.01, 0.01)
con[i,j] = c0 + noise * (0.5 - np.random.rand())
else:
# 如果iflag不等于1，则创建一个长度为NxNy的一维零数组
con = np.zeros(NxNy)
for i in range(Nx):
for j in range(Ny):
ii = i * Nx + j
con[ii] = c0 + noise * (0.5 - np.random.rand())
return concalculate_energ.py
def calculate_energ(Nx,Ny,con,grad_coef):
energ = 0.0
for i in range(Nx-1):
ip = i+1
for j in range(Ny-1):
jp = j+1
energ = (energ + con[i,j]**2 * (1.0 - con[i,j])**2 + 0.5 * grad_coef * ((con[ip,j] - con[i,j])**2 + (con[i,jp] - con[i,j])**2))
return energfree_energ_ch.py
def free_energ_ch_v1(i,j,con):
c = con[i,j]
dfdcon = 2 * c * (1-c) * (1 - 2*c)
return dfdconwrite_vtk_grid_values.py
def write_vtk_grid_values(nx,ny,dx,dy,istep,data1):
fname = f'time_{istep}.vtk'
out = open(fname,'w')
nz = 1
npoin = nx * ny * nz
out.write('# vtk DataFile Version 2.0\n')
out.write(f'time_{istep}.vtk\n')
out.write('ASCII\n')
out.write('DATASET STRUCTURED_GRID\n')
out.write(f'DIMENSIONS {nx:5d} {ny:5d} {nz:5d}\n')
out.write(f'POINTS {npoin:7d} float\n')
for i in range(nx):
for j in range(ny):
x = i * dx
y = j * dy
z = 0.0
out.write(f'{x:14.6e} {y:14.6e} {z:14.6e}\n')
out.write(f'POINT_DATA {npoin:5d}\n')
out.write('SCALARS CON float 1\n')
out.write('LOOKUP_TABLE default\n')
for i in range(nx):
for j in range(ny):
out.write(f'{data1[i,j]:14.6e}\n')
out.close()laplacian.py
import numpy as np
import scipy.sparse as sp # 导入scipy稀疏矩阵模块
from scipy.sparse import kron, eye, diags # 从scipy导入特定的稀疏矩阵函数
def laplacian(nx,ny,dx,dy):
nxny = nx * ny
r = np.zeros(nx)
r[0] = 2
r[1] = -1
T = sp.lil_matrix((nx,nx))
# 创建nx×nx的稀疏矩阵（LIL格式，便于修改）
# 填充T矩阵，构造1D拉普拉斯算子（非周期性）
for i in range(nx):
for j in range(nx):
if i == j:
T[i,j] = 2 # 对角线元素
elif abs(i - j) == 1:
T[i,j] = -1 # 相邻元素
# 将T转换为CSR格式（便于高效的矩阵运算）
T = T.tocsr()
# 创建nx×nx的单位矩阵（CSR格式）
E = eye(nx, format='csr')
# 使用Kronecker积构造2D拉普拉斯算子
# kron(T, E) 对应x方向的二阶导数
# kron(E, T) 对应y方向的二阶导数（原代码中E.T应为笔误，E是方阵转置后不变）
grad = -(kron(T,E) + kron(E,T))
# 将grad转换为LIL格式，便于修改边界条件
grad = grad.tolil()
# 处理周期性边界条件
for i in range(nx):
ii = i * nx
jj = ii + nx -1
grad[ii,jj] = 1.0
grad[jj,ii] = 1.0
# 转换回CSR格式以提高后续运算效率
grad = grad.tocsr()
grad = grad / (dx * dy)
return grad
# LIL 格式：适合构建矩阵（如循环填充元素）或随机修改元素，但不适合大规模数值运算。
# CSR 格式：适合矩阵乘法、切片、与向量的乘积等数值操作，运算效率极高，但修改元素不方便。